Point for improving the performance of PID controllers. It offers an introduction to both the art and the science behind process control and PID controller tuning. Included are basic terminology, steps for analyzing process dynamics, methods for determining model parameters, and other valuable insights. With these fundamentals we. Manual PID tuning is done by setting the reset time to its maximum value and the rate to zero and increasing the gain until the loop oscillates at a constant amplitude. (When the response to an error correction occurs quickly a larger gain can be used. If response is slow a relatively small gain is desirable). There are a lot of tuning mehods for PID control, the main classic methods being Zigler-Nichols, Cohen-Coon and Chien-Hrones-Reswick. This methods are based on first-order-plus-dead-time models. The preferred method is open-loop with the PID controller in manual mode so the CO can be adjusted directly, but it is also possible to use a closed-loop method in automatic mode where the SP is adjusted to create the response.
English • العربية • български • català • čeština • Deutsch • Ελληνικά • español • فارسی • français • hrvatski • magyar • italiano • română • 日本語 • 한국어 • lietuvių • Nederlands • norsk • polski • português • русский • Türkçe • українська • 中文(中国大陆) • 中文(台灣) • עברית • azərbaycanca • |
PID tuning refers to the parameters adjustment of a proportional-integral-derivative control algorithm used in most repraps for hot ends and heated beds.
PID needs to have a P, I and D value defined to control the nozzle temperature. If the temperature ramps up quickly and slows as it approaches the target temperature, or if it swings by a few degrees either side of the target temperature, then the values are incorrect.
To run PID Autotune in Marlin and other firmwares, run the following G-code with the nozzle cold:
This will heat the first nozzle (E0), and cycle around the target temperature 8 times (C8) at the given temperature (S200) and return values for P I and D. An example from http://www.soliwiki.com/PID_tuning is:
For Marlin, these values indicate the counts of the soft-PWM power control (0 to PID_MAX) for each element of the control equation. The softPWM value regulates the duty cycle of the f=(FCPU/16/64/256/2) control signal for the associated heater. The proportional (P) constant Kp is in counts/C, representing the change in the softPWM output per each degree of error. The integral (I) constant Ki in counts/(C*s) represents the change per each unit of time-integrated error. The derivative (D) constant Kd in counts/(C/s) represents the change in output expected due to the current rate of change of the temperature. In the above example, the autotune routine has determined that to control for a temperature of 200C, the soft PWM should be biased to 92 + 19.56*error + 0.71 * (sum of errors*time) -134.26 * dError/dT. The 'sum of errors*time' value is limited to the range +/-PID_INTEGRAL_DRIVE_MAX as set in Configuration.h. Commercial PID controllers typically use time-based parameters, Ti=Kp/Ki and Td=Kd/Kp, to specify the integral and derivative parameters. In the example above: Ti=19.56/0.71=27.54s, meaning an adjustment to compensate for integrated error over about 28 seconds; Td=134.26/19.56=6.86s, meaning an adjustment to compensate for the projected temperature about 7 seconds in the future.
The Kp, Ki, and Kd values can be entered with:
In the case of multiple extruders (E0, E1, E2) these PID values are shared between the extruders, although the extruders may be controlled separately. If the EEPROM is enabled, save with M500. If it is not enabled, save these settings in Configuration.h.
For the bed, use:
Pid Controller Tuning Methods
and save bed settings with:

For manual adjustments:
- if it overshoots a lot and oscillates, either the integral gain needs to be increased or all gains should be reduced
- Too much overshoot? Increase D, decrease P.
- Response too damped? Increase P.
- Ramps up quickly to a value below target temperature (0-160 fast) and then slows down as it approaches target (160-170 slow, 170-180 really slow, etc) temperature? Try increasing the I constant.
See also Wikipedia's PID_controller and Zeigler-Nichols tuning method. Marlin autotuning (2014-01-20, https://github.com/ErikZalm/Marlin/blob/Marlin_v1/Marlin/temperature.cpp#L250 ) uses the Ziegler-Nichols 'Classic' method, which first finds a gain which maximizes the oscillations around the setpoint, and uses the amplitude and period of these oscillations to set the proportional, integral, and derivative terms.
Saving PID settings
You will need to commit your changes to EEPROM or your configuration.h file for them to be permanent.
To save to EEPROM use:M500
Modifying Marlin Autotune parameters
The default Marlin M303 calculates a set of Ziegler-Nichols 'Classic' parameters based on the Ku (Ultimate Gain) and the Pu (Ultimate Period), where the Ku and Pu are determined by searching for a biased BANG-BANG oscillation around an average power level that produces oscillations centered on the setpoint. (See https://github.com/ErikZalm/Marlin/blob/Marlin_v1/Marlin/temperature.cpp#L238 )
You can transform these 'Classic' parameters into the Zeigler-Nichols 'Some Overshoot' set with:
Or the Z-N 'No Overshoot' set:
Note that the multipliers for the autotuning parameters each have only one significant digit (implying 10% maximum precision), and that the other schemes differ by factors of 2 or 3. PID autotuning and tuning isn't terribly precise, and changes in the parameters by factors of 5 to 50% are perfectly reasonable.
In Marlin, the parameters that control and limit the PID controller can have more significant effects than the popular PID parameters. For example, PID_MAX and PID_FUNCTIONAL_RANGE, and PID_INTEGRAL_DRIVE_MAX can each have dramatic, unexpected effects on PID behavior. For instance, a too-large PID_MAX on a high-power heater can make autotuning impossible; a too-small PID_FUNCTIONAL_RANGE can cause odd reset behavior; a too large PID_FUNCTIONAL_RANGE can guarantee overshoot; and a too-small PID_INTEGRAL_DRIVE_MAX can cause droop.
PID Tuning by Commercial PID
If you have access to a PID controller unit and a compatible thermal probe that fits down into your hotend, you can use them to tune your PID and calibrate your thermistor.
Connection of the output of the PID to your heater varies depending on your electronics. (I used a 1K2:4K7 voltage divider to drop the 22V output of the PID to 5V for my bread-boarded VNP4904)
After the PID is connected you can use it to measure the nozzle temperature and correlate it with the thermistor readings and resistances.
Conversion from the commercial PID values of kP in %fullscale, Ti in seconds, and Td in seconds is as follows:
As an example, a $30 MYPIN TD4-SNR 1/16 DIN PID temperature controller and $10 type-K probe can hold a particular Wildseyed hotend with a 6.8ohm resistor at 185.0C+/-0.1C using 12V with about a 43.7% duty cycle, or 0.437*12*12/6.8=9.25W. Invoking the autotuning on the controller produces these parameters: P=0.8%/C, I=27s, D=6.7s. Converting these to Marlin PID values:
Differences between the results can be caused by physical differences in the systems, (e.g: the thermocouple is closer to the heater than the thermistor,) or by different choices of autotuning parameters (e.g.: the MYPIN TD4 autotuning process is a proprietary black box, while Marlin uses Zeigler-Nichols 'Classic' method.)
The Temperature/resistance table below was developed by using the PID+thermocouple system to set temperatures on a sample hotend by controlling the heater while measuring the thermistor resistance. These values can be used with Nophead's http://hydraraptor.blogspot.com/2012/11/more-accurate-thermistor-tables.html or Marlin's https://github.com/ErikZalm/Marlin/blob/Marlin_v1/Marlin/createTemperatureLookupMarlin.py to create calibrated thermistor tables. The PID column collects the autotuning values produced by the PID controller for the indicated temperature. The kP,Ki,Kd lists the converted parameters.
| Temp | DutyCycle | Thermistor R | Commercial PID | Kp,Ki,Kd |
|---|---|---|---|---|
| 60.0 | 6.0 | 31630 | ||
| 100.0 | 15.7 | 10108 | 1.1%/C, 35.5s, 8.8s | 2.81, 0.08, 3.13 |
| 120.0 | 22.5 | 5802 | 1.0%/C, 32.0s, 8.0s | 2.55, 0.08, 3.14 |
| 135.0 | 26.5 | 3967 | ||
| 150.0 | 28.5 | 2840 | 1.2%/C, 29.0s, 7.2s | 3.06, 0.10, 2.35 |
| 170.0 | 34.0 | 1829 | ||
| 185.0 | 43.7 | 1347 | 0.8%/C, 27s, 6.7s | 2.04, 0.08, 3.28 |
| 190.0 | 45.9 | 1200 | 0.8%/C, 26s, 6.5s | 2.04, 0.08, 3.18 |
| 200.0 | 51.0 | 977 |
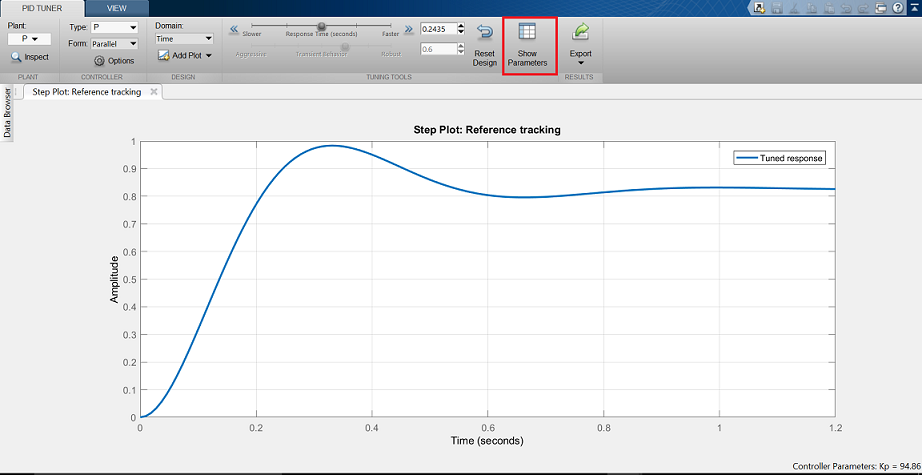
PID tuning is the process of finding the values of proportional, integral, and derivative gains of a PID controller to achieve desired performance and meet design requirements.
PID controller tuning appears easy, but finding the set of gains that ensures the best performance of your control system is a complex task. Traditionally, PID controllers are tuned either manually or using rule-based methods. Manual tuning methods are iterative and time-consuming, and if used on hardware, they can cause damage. Rule-based methods also have serious limitations: they do not support certain types of plant models, such as unstable plants, high-order plants, or plants with little or no time delay.
You can automatically tune PID controllers using software tools to achieve the optimal system design and to meet design requirements, even for plant models that traditional rule-based methods cannot handle well.
For more information on tuning PID controllers automatically, see Control System Toolbox™ for use with MATLAB® and Simulink®.
How To Adjust Pid Settings
An automated PID tuning workflow involves:
Manual Pid Tuning Tips
- Identifying plant model from input-output test data
- Modeling PID controllers (for example, in MATLAB using PID objects or in Simulink using PID Controller blocks)
- Automatically tuning PID controller gains and fine-tuning your design interactively
- Tuning multiple controllers in batch mode
- Tuning single-input single-output PID controllers as well as multiloop PID controller architectures
